Types of Energy!

Chemical Potential Energy

Chemical potential energy is a form of potential energy related to the structural arrangement of atoms or molecules. This arrangement may be the result of chemical bonds within a molecule or otherwise. Chemical energy of a chemical substance can be transformed to other forms of energy by a chemical reaction. However, due to the first law of thermodynamics, this energy can not be created nor destroyed. For example, when a fuel is burned the chemical energy is converted to heat. Also, the digestion of food releases heat. Another example is how plants transform solar energy to chemical energy through the process known as photosynthesis

If something is broken down, the chemical energy is released, usually as heat. If a reaction releases energy, it is called exothermic, and if it absorbs energy, it is called endothermic.

Gravitational Potential Energy

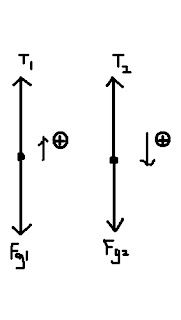
Gravitational energy is the potential energy associated with the force of gravity. It is stored within an object as a result of having height above the Earth's surface. If an object falls from one point to another point inside a gravitational field, the force of gravity will do positive work on the object, and the gravitational potential energy will decrease by the same amount.

For example, consider a book, placed on top of a table. When the book is raised from the floor to the table, some external force works against the gravitational force. If the book falls back to the floor, the same work will be done by the gravitational force. Thus, if the book falls off the table, this potential energy goes to accelerate the mass of the book (and is converted into kinetic energy). When the book hits the floor this kinetic energy is converted into heat and sound by the impact.

The factors that affect an object's gravitational potential energy are its height relative to some reference point, its mass, and the strength of the gravitational field it is in. Thus, a book lying on a table has less gravitational potential energy than the same book on top of a taller cupboard, and less gravitational potential energy than a heavier book lying on the same table. Also, due to Newton's law of gravitation, an object at a certain height above the Moon's surface has less gravitational potential energy than at the same height above the Earth's surface. This is because the Moon's gravity is weaker since it has less mass than the Earth.

In this example, the flower pot on the right has more gravitational potential energy because of its height.

Elastic Potential Energy

Elastic energy is the potential mechanical energy stored in the configuration of a material or physical system as work is performed to distort its volume or shape.

The essence of elasticity is reversibility. Forces applied to an elastic material transfer energy into the material which, upon yielding that energy to its surroundings, can recover its original shape. However, all materials have limits to the degree of distortion they can endure without breaking or becoming permanently deformed. Therefore, when an object is stretched beyond its elastic limit, it is no longer storing all of the energy from mechanical work performed on it in the form of elastic energy.

In this example, the elastic band is storing elastic potential energy as the car is trying to distort its shape

 Mechanical Potential Energy

Mechanical energy is the sum of energy in a mechanical system. This energy includes both kinetic energy, the energy of motion, and potential energy, the stored energy of position. Mechanical energy exists as both kinetic and potential energy in a system. Kinetic energy, the energy of motion, exists whenever an object is in motion. Potential energy is based on the position of an object. It can not cause any change on its own, but it can be converted to other forms of energy. For example, A bowling ball placed high above the ground would possess no kinetic energy. It would, however, possess a large amount of potential energy that would be converted to kinetic energy if the ball were allowed to fall.

Thermal Energy

Thermal energy is generated and measured by heat of any kind. When an object is "hot" or has a lot of thermal energy, the atoms and molecules within the object are "vibrating" more than in a cooler object.

Some people consider thermal energy to be the "heat energy" of a body that it has and that would have to be removed to cool the object to absolute zero. At absolute zero, an object is said to have no thermal energy. If that same body is sitting at 0°C, it is "hotter" than at 0 K. And some amount of thermal energy is necessary to raise that body up to 0°C.

Thermal energy is used in all sorts of ways. We use it to keep warm (by heating structures and vehicles), prepare food (both at home and commercially), and to make millions of products (manufacturing and industrial applications). We can convert thermal energy into electrical energy, too. It is thermal energy from the sun that supports life on this planet. 

Sound Energy

Sound energy is the energy produced by sound vibrations as they travel through a specific medium. Sound vibrations cause waves of pressure which lead to some level of compression and rarefaction in the mediums through which the sound waves travel. Sound energy is, therefore, a form of mechanical energy; it is not contained in discrete particles and is not related to any chemical change, but is purely related to the pressure its vibrations cause. Sound energy is typically not used for electrical power or for other human energy needs because the amount of energy that can be gained from sound is quite small.

Rather than measuring sound in typical units of energy, such as joules, scientists and others tend to measure it in terms of pressure and intensity using units such as pascals and decibels. Sound measurements are, by their very nature, relative to other sounds that cause more or less pressure. Usually, sound is described in terms of the way it is perceived by healthy human ears. A sound that produces 100 pascals of pressure at an intensity level of about 135 decibels is, for example, commonly described as the threshold of pain. It is of adequate pressure and intensity, often combined into the common term "loudness," to cause physical pain.

CANNONS!

One of the most recognizable structures in human history, the cannon is considered by some to be the pinnacle of warfare artillery. However, behind its thick shell and stern reputation lies an engineering marvel. It might seem strange, but physics is the backbone of the cannon.

A complicated cannon; assembled in a manner so that it remains hidden behind a barricade

As a project, our class will be building cannons on Thursday. The materials are a maximum of 5 soda cans, duct tape, and two Styrofoam cups. First of all, I believe that the cannon will be more successful if we make sure the inner part of the cannon is very smooth. This reduces the amount of friction that the cannon ball will experience. Also, the cannon barrel should be quite long, instead of very short. This way, the cannon ball will not experience as much air resistance when it leaves the cannon. Regarding the cannon ball itself, it might not actually have to be a ball. Looking at fast airplanes and cars, it seems that the most prevalent form of aerodynamic structure is a pointed tip. For example, F15 fighter jets are designed so that they are highly aerodynamic. The reason that these airplanes are so aerodynamic is because of their shape. When moving through the air, air resistance will be evenly distributed along the airplane rather than hitting it with a very strong force. (Newton's third law: every action has an opposite and equal reaction).

F15 Silent Eagle fighter jet

Now, for the angle of the cannon. In the kinematics unit, we learned about projectile motion. We learned the equation:

In this equation, d is the horizontal distance traveled, v is the velocity of the projectile and g is the force of gravity. From looking at this equation, we can already determine that the largest angle at which the cannon can be fired is 90°. This is because anything greater than that will result in a cannon that shoots straight upward or backwards (in other words a cannon that is not fit for combat). Thus, the angle must be less than 90°. But what angle will allow us to maximize the distance traveled? This is where the equation comes into place. 

Isolate sin2theta.

Using this equation, another clue is found. It appears that if theta = 45°, then the d will be be maximized. 
Since sin (45x2) = sin 90=1, therefore 45° will likely produce the farthest distance traveled.

This is because if theta=45°, then 2xtheta would equal 90°.

 

Newton's Problems

Lately we have been doing some extensive work on an interesting fellow called Sir Isaac Newton.

 

First of all, who is Newton? According to Encylcopedia Britannica, Newton was a English physicist, mathematician, astronomer and philosopher. He is also considered by many people to be one of the most influential people in human history. Throughout his lifetime, he discovered many new things and created new scientific laws. Among which were his three laws of motion:

1st Law: Inertia
Inertia is a term used by people to describe the tendency for an object to resist a change in motion. In everyday terms, the 1st law can be basically simplified into this: an object at rest will stay at rest, forever, as long as nothing pushes or pulls on it. An object in motion will stay in motion, traveling in a straight line, forever, until something pushes or pulls on it. In other words, objects will maintain their motion stationary or moving unless there is an external force. For example, beginner ice skaters find it difficult to stop their motion, unless they crash or fall.

2nd Law: F, m, a
Newton found that force, mass, and acceleration are all related. His second law states that: the acceleration of an object depends inversely on its mass and directly on the unbalanced force applied to it. This creates the equation:

3rd Law: Action=Reaction

Newton's third law applies to an action and a reaction. His law states that: for every action, there is an equal & opposite reaction. Take for example a a person standing on the ground. He is not moving vertically at all. Why does this happen? It happens because there are two forces acting on it and they are equal. First, gravity is applied to the person. However, there is a force that is opposite to gravity operating at the same intensity: the normal force. The third law applies.




Newton Problems
Newton's three laws apply to a plethora of things in this universe. As a result, it is only natural that questions and problems are formed. In this unit, we focus on four types of Newton Problems: Equilibrium, Incline (kinetic and static), Pulley, and Train.

Equilibrium

Assumptions

-no friction

-set positive axes

-Tix=Tiy

a=0            

F= ma 
X component
Fₓ = ma                                                                                 

T1ₓ - T2ₓ = 0                                               

T1ₓ = T2ₓ      

Y component  

Fy = ma   
-Fg + T1y + T2y = 0
T1y + T2y = Fg

T1sinB + T2sinA = mg

 (T1sinB + T2sinA) / g = m

 

Inclines

STATIC(object not moving)

Assumptions

- fs = µFn

- a = 0

- +ve axes in the direction of decline
- no air resistance

 

KINETIC(object moving)

Assumptions

- fk = µkFn

- aₓ ≠ 0, ay = 0
- +ve in the direction of a

- no air resistance

 

F=ma

 Y component

Fy = ma
Fy = 0
Fn - Fgy = 0
Fn = Fgy
Fn = Fgcosθ
Fn = mgcosθ
X component

Fₓ = maₓ      

Fgₓ - f = maₓ

Fgsinθ - µFn = maₓ        

mgsinθ - µmgcosθ = maₓ

(mgsinθ - µmgcosθ) / m = aₓ

 

Pulleys

Assumptions

- frictionless pulleys + rope

- no air resistance

- multiple FBDs

- positive in direction of a

- T1 = T2

- a of the system is the same

 

to find m1

F = ma

Fₓ = ma

Fₓ = 0

Fy = m1ay

m1g - T = m1a (1)

to find m2

F = ma

Fₓ = ma

Fₓ = 0

Fy = m2ay

T - m2g = m2ay (2)

Find a

From (1) T = m1g - m1a    (3)

From (2) T = m2a + m2g   (4)

m1g - m1a = m2a + m2g

m1g - m2g = m2a + m1a

m1g - m2g = a (m2 + m1)

(m1g - m2g) / (m2 + m1) = a

 

Simplified FBD of train system (applies only to a)

Trains

Assumptions

- 1 FBD for a

- 3 FBDs for T1 and T2

- ay = 0

- a is consistent

- no air resistance
- weightless cables

- positive in direction of a

 

F = ma

X component

Fₓ = maₓ

Fₐ - f = maₓ 

Fₐ - µmg = maₓ

(Fₐ - µmg) / m = aₓ

Y Component
Fy = may
Fy = 0
Fn - mg = 0
Fn = mg

Projectile Motion

Projectile motion is one of the most important yet basic studies in physics. It can be described as a collaboration between the Big 5 problems and vector components. This is because it is recommended that these complicated questions be simplified by splitting the values into x and y components. (Knowledge of trigonometry is also recommended/needed.) There are 4 main types of projectile motion questions that you will likely encounter in Grade 11 physics:

Type 1:

In this case, an object starts off above its destination, and due to the force of gravity it falls. In most cases, the acceleration in y, or gravity, is 9.81. In type 1 questions, there is no acceleration for x, since there is no air resistance or opposing horizontal force. Therefore, Vx is also constant. In most scenarios for type 1 questions, the time is found first. Then, by substituting the time into an equation, other variables can be found, most often the distance in x or y.

Type 2

In type 2 questions, the acceleration in x is 0, like in type 1 questions. Also, there is gravity, but it is negative. Usually, and angle is given. Then, using sin and cos, the initial horizontal and vertical velocities can be found. To calculate the initial horizontal velocity, use the equation V1cos(theta). To calculate the initial vertical velocity, use the equation V1sin(theta). Also, in type 2 questions, R represents the horizontal distance and h represents the the maximum height. The unique part of type 2 questions is that dy is 0. As you can see from the diagram, the projectile begins and ends at ground level.

Type 3

In type 3 questions, everything is almost identical
to the type 2 questions. However, in this case, the projectile does not end at ground level. In this case, it landed on something. This object has a height, and usually it is this variable that we must calculate. Keep in mind that the height of this object is the dy, and it is positive. An example of a type 3 question is whether a baseball thrown at a certain angle will be able to pass a 3m tall object 15m away.

Type 4

In type 4 questions, everything is identical to type 3 questions except for one thing: now, the projectile is fired from a height that is higher than its estimated landing position. In this case, the dy is negative, because it is lower than the starting position. An example of a type 4 question is how far a rock will go if thrown at an angle from a 200m cliff.


Now that you know the four main types of projectile motion problems, there is only one thing you can do: Practice!

If you need help, you can use this website: http://cnx.org/content/m13856/latest/

Physics of Roller Coasters

Roller coasters are some of the most thrilling rides in the world. The feeling of weightlessness, the anticipation, and the thrill are some of the reasons for its universal appeal. However, for the average layman, the journey ends once he gets off the roller coaster. We, as physics students, must take the next step: find out how the roller coaster works.

In a nutshell, roller coasters utilize two main forces: kinetic energy, and potential energy. The reason that most roller coasters start off from a very high point is so it can build up its potential energy. In other words, the higher the elevation, the more distance that gravity can pull the coaster down. Then, as the roller coaster goes down the hill, the potential energy is transformed into kinetic energy (the energy that takes you downwards.) After that, the roller coaster once again builds up its potential energy by going up another hill. As you can see, the roller coaster is actually continuously transforming potential energy to kinetic energy and vice versa.

My favorite roller coaster is the Behemoth at Canada's Wonderland, and it is a great example of a roller coaster transforming energy.

How to Add Vectors!

It seems that vectors is just one of those words that strikes fear in many students old and young alike. However, with the right fundamentals and techniques, the subject of vectors can be conquered without either extraordinary mathematics skills nor knowledge of physics. Before one can begin learning about vectors, he/she must first learn what a vector is. According to the Merriam Webster Dictionary, a vector is a variable quantity that can be resolved into component. To simplify this, here is an actual vector: 

A vector has three types of information: 1. the length
                                                            2. the angle
                                                            3. the direction


Now that we know what a vector is and what it signifies, we can start to conduct simple addition question for vectors.


If the vectors that we are adding have a distinct direction (North, South, East or West), then we just connect them. 

As you can see from this picture, the addition of vectors usually results in an imaginary triangle. After adding the horizontal component and the vertical component, you connect the origin to the ending point using a straight line. The first thing that you will need to calculate is the length of the hypotenuse. Due to the fact that you will know the lengths of the horizontal and vertical vectors, you can apply the Pythagorean Theorem:

Once you finish that, you will have the length of the vector. However, as I stated earlier, a vector has three components. Length is only one of the components. We also have to find the direction and the angle. To find the angle, we must measure angles with respect to North and South. If you are confused, simply draw a cross at the origin to display to you North, South, East and West. Now, you must apply simple trigonometry. Once you find out the right angle to measure, you can use tan, which is the length of the opposite side divided by the length of the adjacent side. Finally, you will have the angle. The last step is to simply state what direction the vector is going. To do this, you just need to look at the angle that you previously discovered. Since the angles are measured with respect to North and South, simply write East/West of North/South (whichever ones apply to your question)


Your end result should look somewhat like this: x=__m (N__ E)


And that's all you need to know about vectors for now!

Deriving Equation 4 from the Graph

Equation #4 is: d=V2Δt-½aΔt²

In order to derive the equation from the graph, we must find the area between the slope and the x axis. Unlike the steps for Equation 3, this time we must first find the area of the large rectangle and then subtract the smaller triangle from it.


The equation for the rectangle is ab, where a = base, and b= height. From the graph, we can determine the base and height of the rectangle. The length is Δt and the height is V2.

So, area of rectangle=V2(Δt)

To find the area of the triangle, we know that the equation is ab/2, where a is the base and b is the height. For the small triangle that we are going to use, it appears that its height is V2-V1, and its length is Δt.

So, area of triangle=½(V2-V1)Δt
                           
From Equation 1, we find that aΔt=V2-V1!

Substituting that into the equation gives us the following:

area of triangle=(½aΔt)Δt
                      = ½aΔt²

Finally, by subtracting the area of the triangle from the area of the rectangle, this gives us equation 4: 

d=V2Δt-½aΔt²

Deriving Equation 3 from the Graph

Equation 3 is: d=vΔt+½aΔt²

From the graph, we have V2, V1, t1, and t2.

In order to calculate the displacement, we have to find the area. We can do this in two ways: we can find the area of the triangle and the square, or we can find the area of the entire trapezoid. For this instance, I am going to find the area of the triangle and the rectangle.

The equation for calculating the area of a rectangle is a times b, where a is the height and b is the width.

From the graph, we can see that a=V1, and b=t2-t1.

So, A=(ab)
      A=V1(t2-t1)
      A=V1(Δt)

Now, we have to find the area of the triangle. The equation is a times b divided by 2, where a is the height and b is the length of the base. From this equation, we can find that it can also be expressed as 1/2ab.

From the graph, the base is Δt, and the height is V2-V1.

So, A=1/2Δt(V2-V1)

From Equation #1, we know that V2-V1= aΔt.

Therefore, A=1/2Δt(aΔt)
                 A=1/2aΔt²

So, because d(displacement)=area
Therefore finally, d=vΔt+½aΔt².

Translating Graphs from the Experiment

Here are the 6 graphs which have been translated. (Graph pictures courtesy of Daniel)

Graph 1 (Distance vs. Time)

1. Stay and don't move at a distance of 1m for 1 second.

2. Walk 1.5m in 2 seconds (0.75 m/s) away from the origin.

3. Stay at 2.5m for 3 seconds.

4. Walk 0.75m in 1.5 seconds (0.5 m/s) back towards the origin.

5. Stay at 1.75m for 2.5 s.

Graph 2 (Distance vs. Time)

1. Begin at a distance of 3m away from the origin. Walk back towards the origin at a rate of 1.5m in 3 s (0.5 m/s)

2. Stay at a distance of 1.5m for 1 s.

3. Jog back towards the origin at a rate of1m in 1 second (1 m/s).

4. Stay at a distance of 0.5m for 2 s.

5. Jog away from the origin at a rate of 2.5m in 3 seconds (0.83 m/s)



Graph 3 (Velocity vs. Time)

1. Don't move for 2 seconds.
2. Walk away from the origin at 0.5 m/s for 3 seconds
3. Stay still for 2 seconds.
4. Walk towards the origin at 0.5 m/s for 3 seconds.

Graph 4 (Velocity vs. Time)

1. Accelerate at 0.5 m/s in 4 seconds away from the origin.

2. Continue walking away from the origin at 0.5 m/s for 2 seconds.

3. Walk back towards the origin at 0.4 m/s for 3 seconds.

4. Stop and don't move for 1 second.

Graph 5 (Distance vs. Time)

1. Start at a distance of approximately 0.8m from the origin and walk away at a rate of 1m in 3.5 s (0.29 m/s)

2. Stay still at a distance of 1.8m for 3.25 s.

3. Continue walking away from the origin at a rate of 1.4m in 2.25 s (0.62 m/s)

Graph 6 (Velocity vs. Time)

1. Walk away from the origin at roughly 0.35 m/s for 3 seconds.

2. Walk back towards the origin at roughly 0.35 m/s for 3.5 seconds.

3. Don't move for 3.5 seconds.

Motor Lab

Day 1: Today, we had our motor lab project. The goal was to build an electric motor that could spin a minimum of 3 complete rotations. My partner Steven and I began our project by first getting a piece of wood which we made sure was not compressed. Then, we used nails and a hammer to puncture 4 nails in the wood. The 4 nails were assembled in a square shape, with a nail at each corner. The square's dimension's were approximately 3cm long by 5 cm wide. While I hammered the four nails into the wood, Steven used sandpaper to sand the strips of aluminum, which would eventually become our brushes. Our next step was to assemble the cork, the axel, and the commutator pins. We did this by penetrating the middle of the cork with the axel (a thin wooden stick). Then, on the sides of the cork, we screwed in the two commutator pins. Our main obstacle during this step was puncturing holes into the cork: we were afraid that the cork would crack or break, so we hammered very lightly. Next, we used two paper clips to create the bearings, which would be used to hold up and support the axel and the cork. We achieved this by bending the paper clips into the desired shape and then manually sticking them into the wood. The next step was of extreme importance. We had to assemble the wire onto the cork and commutator pins so that it would be able to perform properly. There were three crucial rules of the assembly that we had to follow: a)the wires must be bared using sandpaper, b)the wire must be wrapped around the cork perpendicular to the commutator pins and c)the position of the commutator pins must be accurate. We made sure that we met all three of the criteria and then continued to the final step: assembling the brushes. To do this, we used the previously sanded aluminum strips as well as two thumb tacks. We placed them so that both of the strips would be in contact with the commutator pins. With all of the steps complete, we had just one last thing to do: test the motor out. We marched to Mr. Chung's table, just as another group's motor passed the test with flying colours. Mr. Chung assembled the magnets and connected the wires to our motor. We watched with great anticipation as he flicked the switch. Then, to our horror, our motor spinned once and then stopped moving completely! It was a complete failure. Though it wasn't clear why our motor failed, I suspect that it might have been caused by a combination of many small problems. Mr. Chung suggested that we should cut the brushes shorter and make them more sturdy. We quickly made the changes, but unfortunately it was time for class to end. Fortunately, we have some time tomorrow to do some further testing and we hope that our motor will work this time!   

Day 2: We were very eager to improve our motor for another attempt. This time, we were extremely careful; we meticulously searched the motor for any signs of damage/ misplacement. We reinforced all the materials and also fully sanded the brushes. Since we knew that this was our second and final attempt, we made sure that everything was perfect. Before we went to Mr. Chung to test the motor, we first asked a few of our classmates to look our motor over, since their motors had been successful. After they examined our motor and said that it was good, we went to Mr. Chung for the test. We held our breaths as he attached the wire. To our relief, the motor worked, and it spun. In fact, it was arguably the most successful motor in the class: it spun very quickly and evenly. It was a great feeling for both me and my partner, as all our hard work had finally paid off. 

 

RHR #1and #2

Scientists have developed several hand signs to help you predict how magnetic forces act. They are called right hand rules because they involve using your right hand.

RIGHT HAND RULE #1 (RHR#1) FOR CONVENTIONAL CURRENT FLOW:  Grasp the conductor with the thumb of the right hand pointing in the direction of the conventional, or positive, current flow. The curved fingers point in the direction of the magnetic field around the conductor.

RIGHT HAND RULE #2 (RHR#2) FOR CONVENTIONAL CURRENT FLOW: Grasp the coiled conductor with the right hand such that curved fingers point in the direction of conventional, or positive, current flow. The thumb points in the direction of the magnetic field within the coil. Outside the coil, the thumb represents the north (N) end of the electromagnet produced by the coil.

 For more information please visit:http://physicsed.buffalostate.edu/SeatExpts/resource/rhr/rhr.htm

Notes from P. 582 to 587

Here are my notes on the pages from 582 to 587:

-a magnetic field is the distribution of a magnetic force in the region of a magnet.

-there are two different magnetic characteristics, labelled north and south.

 
SIMILAR MAGNETIC POLES , NORTH AND NORTH OR SOUTH AND SOUTH, REPEL ONE ANOTHER WITH A FORCE AT A DISTANCE. DISSIMILAR POLES, NORTH AND SOUTH, ATTRACT ONE ANOTHER WITH A FORCE AT A DISTANCE.

-a test compass is a gadget we use to map a magnetic field.

-Earth acts like a giant permanent magnet, producing its own magnetic field.

-Ferromagnetic metals are metals that attract magnets. It appears that all magnets are mad up of these materials. They are: Iron, Nickel, and Cobalt, or mixtures of the three.

DOMAIN THEORY: ALL LARGE MAGNETS ARE MADE UP OF MANY SMALLER AND ROTATABLE MAGNETS, CALLED DIPOLES, WHICH CAN INTERACT WITH OTHER DIPOLES CLOSE BY. IF DIPOLES LINE UP, THEN A SMALL MAGNETIC DOMAIN IS PRODUCED.

OERSTED'S PRINCIPLE: CHARGE MOVING THROUGH A CONDUCTOR PRODUCES A CIRCULAR MAGNETIC FIELD AROUND THE CONDUCTOR.

 -Mapping the magnetic field allows you to predict the direction of the electromagnetic force from the current. Scientists have developed several hand signs to help you predict how magnetic forces act. They are called right hand rules because they involve using your right hand.

RIGHT HAND RULE #1 (RHR#1) FOR CONVENTIONAL CURRENT FLOW:  Grasp the conductor with the thumb of the right hand pointing in the direction of the conventional, or positive, current flow. The curved fingers point in the direction of the magnetic field around the conductor.

-If the wire is coiled, the individual field lines fall on top of each other, thereby strengthening the overall field. Coiling the wire in a linear cylinder also straightens out the field.

RIGHT HAND RULE #2 (RHR#2) FOR CONVENTIONAL CURRENT FLOW: Grasp the coiled conductor with the right hand such that curved fingers point in the direction of conventional, or positive, current flow. The thumb points in the direction of the magnetic field within the coil. Outside the coil, the thumb represents the north (N) end of the electromagnet produced by the coil.

Here are some websites that talk about magnetics:
1.http://www.school-for-champions.com/science/magnetism.htm
2.http://www-spof.gsfc.nasa.gov/Education/Imagnet.html

Also, a very cool and easy to understand video:
Introduction to Magnetism

Notes from Page 553-563

Here are my notes for the pages 553-563.

-The amount of current flow in a circuit, and therefore the amount of energy transferred to any useful device depends on two things:
1. The potential difference of the power supply (amount of push)
2. the nature of the pathway through the loads that are using the electric potential energy.

-The more difficult the path, the more opposition there is to a flow.

-The measure of the opposition of flow is called electric resistance.

To measure resistance:

R=V/I

where R is the resistance in volts/ ampere (ohm)
V is the potential difference in volts
I is the resulting current in amperes

-A thinner wire has a larger resistance than a thicker one.

-Ohm found that the V/I ratio was constant for a particular resistor. This law is called the Ohm's Law.

-----------------------------------------------------------------------------------------------------------------------------------------

 Factors that Affect Resistance

-The longer the conductor, the greater the resistance. Factor: Length

-The larger the thickness of the conductor, the less resistance there is. Factor: Cross-sectional area

-Some materials are better conductors than others. Factor: Type of material

-Higher temperatures tend to increase the resistance. Factor: Temperature
------------------------------------------------------------------------------------------------------------------

Kirchhoff's current law: The total amount of current into a junction point of a circuit equals the total current that flows out of that same junction.

Kirchhoff's voltage law: The total of all electrical potential decreases in any complete circuit loop is equal to any potential increases in that circuit loop.

-In any circuit, there is no net gain or loss of energy or electric charge.

Here are some links I found helpful:
1. http://www.the12volt.com/ohm/ohmslaw.asp
2. http://cnx.org/content/m0015/latest/
3. http://physics.about.com/od/electromagnetics/f/KirchhoffRule.htm

Here is a video for Ohm's Law:
http://www.youtube.com/watch?v=_-jX3dezzMg

and one for Kirchhoff's Law:
http://www.youtube.com/watch?v=Mc_g26ixTtA

Ohm's Law Prelab : Chart

Name	Symbol	Unit		Definition
Voltage	V	Volts (V)		A representation of the electric potential energy per unit charge.
Current	I	Amperes (A)		The total amount of charge moving past a point in a conductor, divided by time taken.
Resistance	R	Ohms (Ω)		A measure of the opposition to current flow.
Power	P		Watts (W)	The rate at which work is done.