Physics of Roller Coasters

Roller coasters are some of the most thrilling rides in the world. The feeling of weightlessness, the anticipation, and the thrill are some of the reasons for its universal appeal. However, for the average layman, the journey ends once he gets off the roller coaster. We, as physics students, must take the next step: find out how the roller coaster works.

In a nutshell, roller coasters utilize two main forces: kinetic energy, and potential energy. The reason that most roller coasters start off from a very high point is so it can build up its potential energy. In other words, the higher the elevation, the more distance that gravity can pull the coaster down. Then, as the roller coaster goes down the hill, the potential energy is transformed into kinetic energy (the energy that takes you downwards.) After that, the roller coaster once again builds up its potential energy by going up another hill. As you can see, the roller coaster is actually continuously transforming potential energy to kinetic energy and vice versa.

My favorite roller coaster is the Behemoth at Canada's Wonderland, and it is a great example of a roller coaster transforming energy.

How to Add Vectors!

It seems that vectors is just one of those words that strikes fear in many students old and young alike. However, with the right fundamentals and techniques, the subject of vectors can be conquered without either extraordinary mathematics skills nor knowledge of physics. Before one can begin learning about vectors, he/she must first learn what a vector is. According to the Merriam Webster Dictionary, a vector is a variable quantity that can be resolved into component. To simplify this, here is an actual vector: 

A vector has three types of information: 1. the length
                                                            2. the angle
                                                            3. the direction


Now that we know what a vector is and what it signifies, we can start to conduct simple addition question for vectors.


If the vectors that we are adding have a distinct direction (North, South, East or West), then we just connect them. 

As you can see from this picture, the addition of vectors usually results in an imaginary triangle. After adding the horizontal component and the vertical component, you connect the origin to the ending point using a straight line. The first thing that you will need to calculate is the length of the hypotenuse. Due to the fact that you will know the lengths of the horizontal and vertical vectors, you can apply the Pythagorean Theorem:

Once you finish that, you will have the length of the vector. However, as I stated earlier, a vector has three components. Length is only one of the components. We also have to find the direction and the angle. To find the angle, we must measure angles with respect to North and South. If you are confused, simply draw a cross at the origin to display to you North, South, East and West. Now, you must apply simple trigonometry. Once you find out the right angle to measure, you can use tan, which is the length of the opposite side divided by the length of the adjacent side. Finally, you will have the angle. The last step is to simply state what direction the vector is going. To do this, you just need to look at the angle that you previously discovered. Since the angles are measured with respect to North and South, simply write East/West of North/South (whichever ones apply to your question)


Your end result should look somewhat like this: x=__m (N__ E)


And that's all you need to know about vectors for now!

Deriving Equation 4 from the Graph

Equation #4 is: d=V2Δt-½aΔt²

In order to derive the equation from the graph, we must find the area between the slope and the x axis. Unlike the steps for Equation 3, this time we must first find the area of the large rectangle and then subtract the smaller triangle from it.


The equation for the rectangle is ab, where a = base, and b= height. From the graph, we can determine the base and height of the rectangle. The length is Δt and the height is V2.

So, area of rectangle=V2(Δt)

To find the area of the triangle, we know that the equation is ab/2, where a is the base and b is the height. For the small triangle that we are going to use, it appears that its height is V2-V1, and its length is Δt.

So, area of triangle=½(V2-V1)Δt
                           
From Equation 1, we find that aΔt=V2-V1!

Substituting that into the equation gives us the following:

area of triangle=(½aΔt)Δt
                      = ½aΔt²

Finally, by subtracting the area of the triangle from the area of the rectangle, this gives us equation 4: 

d=V2Δt-½aΔt²

Deriving Equation 3 from the Graph

Equation 3 is: d=vΔt+½aΔt²

From the graph, we have V2, V1, t1, and t2.

In order to calculate the displacement, we have to find the area. We can do this in two ways: we can find the area of the triangle and the square, or we can find the area of the entire trapezoid. For this instance, I am going to find the area of the triangle and the rectangle.

The equation for calculating the area of a rectangle is a times b, where a is the height and b is the width.

From the graph, we can see that a=V1, and b=t2-t1.

So, A=(ab)
      A=V1(t2-t1)
      A=V1(Δt)

Now, we have to find the area of the triangle. The equation is a times b divided by 2, where a is the height and b is the length of the base. From this equation, we can find that it can also be expressed as 1/2ab.

From the graph, the base is Δt, and the height is V2-V1.

So, A=1/2Δt(V2-V1)

From Equation #1, we know that V2-V1= aΔt.

Therefore, A=1/2Δt(aΔt)
                 A=1/2aΔt²

So, because d(displacement)=area
Therefore finally, d=vΔt+½aΔt².

Translating Graphs from the Experiment

Here are the 6 graphs which have been translated. (Graph pictures courtesy of Daniel)

Graph 1 (Distance vs. Time)

1. Stay and don't move at a distance of 1m for 1 second.

2. Walk 1.5m in 2 seconds (0.75 m/s) away from the origin.

3. Stay at 2.5m for 3 seconds.

4. Walk 0.75m in 1.5 seconds (0.5 m/s) back towards the origin.

5. Stay at 1.75m for 2.5 s.

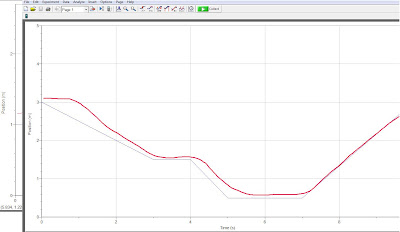Graph 2 (Distance vs. Time)

1. Begin at a distance of 3m away from the origin. Walk back towards the origin at a rate of 1.5m in 3 s (0.5 m/s)

2. Stay at a distance of 1.5m for 1 s.

3. Jog back towards the origin at a rate of1m in 1 second (1 m/s).

4. Stay at a distance of 0.5m for 2 s.

5. Jog away from the origin at a rate of 2.5m in 3 seconds (0.83 m/s)



Graph 3 (Velocity vs. Time)

1. Don't move for 2 seconds.
2. Walk away from the origin at 0.5 m/s for 3 seconds
3. Stay still for 2 seconds.
4. Walk towards the origin at 0.5 m/s for 3 seconds.

Graph 4 (Velocity vs. Time)

1. Accelerate at 0.5 m/s in 4 seconds away from the origin.

2. Continue walking away from the origin at 0.5 m/s for 2 seconds.

3. Walk back towards the origin at 0.4 m/s for 3 seconds.

4. Stop and don't move for 1 second.

Graph 5 (Distance vs. Time)

1. Start at a distance of approximately 0.8m from the origin and walk away at a rate of 1m in 3.5 s (0.29 m/s)

2. Stay still at a distance of 1.8m for 3.25 s.

3. Continue walking away from the origin at a rate of 1.4m in 2.25 s (0.62 m/s)

Graph 6 (Velocity vs. Time)

1. Walk away from the origin at roughly 0.35 m/s for 3 seconds.

2. Walk back towards the origin at roughly 0.35 m/s for 3.5 seconds.

3. Don't move for 3.5 seconds.