Newton's Problems

Lately we have been doing some extensive work on an interesting fellow called Sir Isaac Newton.

 

First of all, who is Newton? According to Encylcopedia Britannica, Newton was a English physicist, mathematician, astronomer and philosopher. He is also considered by many people to be one of the most influential people in human history. Throughout his lifetime, he discovered many new things and created new scientific laws. Among which were his three laws of motion:

1st Law: Inertia
Inertia is a term used by people to describe the tendency for an object to resist a change in motion. In everyday terms, the 1st law can be basically simplified into this: an object at rest will stay at rest, forever, as long as nothing pushes or pulls on it. An object in motion will stay in motion, traveling in a straight line, forever, until something pushes or pulls on it. In other words, objects will maintain their motion stationary or moving unless there is an external force. For example, beginner ice skaters find it difficult to stop their motion, unless they crash or fall.

2nd Law: F, m, a
Newton found that force, mass, and acceleration are all related. His second law states that: the acceleration of an object depends inversely on its mass and directly on the unbalanced force applied to it. This creates the equation:

3rd Law: Action=Reaction

Newton's third law applies to an action and a reaction. His law states that: for every action, there is an equal & opposite reaction. Take for example a a person standing on the ground. He is not moving vertically at all. Why does this happen? It happens because there are two forces acting on it and they are equal. First, gravity is applied to the person. However, there is a force that is opposite to gravity operating at the same intensity: the normal force. The third law applies.




Newton Problems
Newton's three laws apply to a plethora of things in this universe. As a result, it is only natural that questions and problems are formed. In this unit, we focus on four types of Newton Problems: Equilibrium, Incline (kinetic and static), Pulley, and Train.

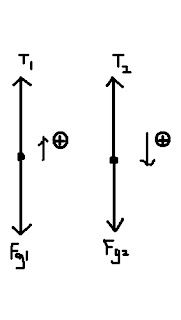
Equilibrium

Assumptions

-no friction

-set positive axes

-Tix=Tiy

a=0            

F= ma 
X component
Fₓ = ma                                                                                 

T1ₓ - T2ₓ = 0                                               

T1ₓ = T2ₓ      

Y component  

Fy = ma   
-Fg + T1y + T2y = 0
T1y + T2y = Fg

T1sinB + T2sinA = mg

 (T1sinB + T2sinA) / g = m

 

Inclines

STATIC(object not moving)

Assumptions

- fs = µFn

- a = 0

- +ve axes in the direction of decline
- no air resistance

 

KINETIC(object moving)

Assumptions

- fk = µkFn

- aₓ ≠ 0, ay = 0
- +ve in the direction of a

- no air resistance

 

F=ma

 Y component

Fy = ma
Fy = 0
Fn - Fgy = 0
Fn = Fgy
Fn = Fgcosθ
Fn = mgcosθ
X component

Fₓ = maₓ      

Fgₓ - f = maₓ

Fgsinθ - µFn = maₓ        

mgsinθ - µmgcosθ = maₓ

(mgsinθ - µmgcosθ) / m = aₓ

 

Pulleys

Assumptions

- frictionless pulleys + rope

- no air resistance

- multiple FBDs

- positive in direction of a

- T1 = T2

- a of the system is the same

 

to find m1

F = ma

Fₓ = ma

Fₓ = 0

Fy = m1ay

m1g - T = m1a (1)

to find m2

F = ma

Fₓ = ma

Fₓ = 0

Fy = m2ay

T - m2g = m2ay (2)

Find a

From (1) T = m1g - m1a    (3)

From (2) T = m2a + m2g   (4)

m1g - m1a = m2a + m2g

m1g - m2g = m2a + m1a

m1g - m2g = a (m2 + m1)

(m1g - m2g) / (m2 + m1) = a

 

Simplified FBD of train system (applies only to a)

Trains

Assumptions

- 1 FBD for a

- 3 FBDs for T1 and T2

- ay = 0

- a is consistent

- no air resistance
- weightless cables

- positive in direction of a

 

F = ma

X component

Fₓ = maₓ

Fₐ - f = maₓ 

Fₐ - µmg = maₓ

(Fₐ - µmg) / m = aₓ

Y Component
Fy = may
Fy = 0
Fn - mg = 0
Fn = mg

Projectile Motion

Projectile motion is one of the most important yet basic studies in physics. It can be described as a collaboration between the Big 5 problems and vector components. This is because it is recommended that these complicated questions be simplified by splitting the values into x and y components. (Knowledge of trigonometry is also recommended/needed.) There are 4 main types of projectile motion questions that you will likely encounter in Grade 11 physics:

Type 1:

In this case, an object starts off above its destination, and due to the force of gravity it falls. In most cases, the acceleration in y, or gravity, is 9.81. In type 1 questions, there is no acceleration for x, since there is no air resistance or opposing horizontal force. Therefore, Vx is also constant. In most scenarios for type 1 questions, the time is found first. Then, by substituting the time into an equation, other variables can be found, most often the distance in x or y.

Type 2

In type 2 questions, the acceleration in x is 0, like in type 1 questions. Also, there is gravity, but it is negative. Usually, and angle is given. Then, using sin and cos, the initial horizontal and vertical velocities can be found. To calculate the initial horizontal velocity, use the equation V1cos(theta). To calculate the initial vertical velocity, use the equation V1sin(theta). Also, in type 2 questions, R represents the horizontal distance and h represents the the maximum height. The unique part of type 2 questions is that dy is 0. As you can see from the diagram, the projectile begins and ends at ground level.

Type 3

In type 3 questions, everything is almost identical
to the type 2 questions. However, in this case, the projectile does not end at ground level. In this case, it landed on something. This object has a height, and usually it is this variable that we must calculate. Keep in mind that the height of this object is the dy, and it is positive. An example of a type 3 question is whether a baseball thrown at a certain angle will be able to pass a 3m tall object 15m away.

Type 4

In type 4 questions, everything is identical to type 3 questions except for one thing: now, the projectile is fired from a height that is higher than its estimated landing position. In this case, the dy is negative, because it is lower than the starting position. An example of a type 4 question is how far a rock will go if thrown at an angle from a 200m cliff.


Now that you know the four main types of projectile motion problems, there is only one thing you can do: Practice!

If you need help, you can use this website: http://cnx.org/content/m13856/latest/

Physics of Roller Coasters

Roller coasters are some of the most thrilling rides in the world. The feeling of weightlessness, the anticipation, and the thrill are some of the reasons for its universal appeal. However, for the average layman, the journey ends once he gets off the roller coaster. We, as physics students, must take the next step: find out how the roller coaster works.

In a nutshell, roller coasters utilize two main forces: kinetic energy, and potential energy. The reason that most roller coasters start off from a very high point is so it can build up its potential energy. In other words, the higher the elevation, the more distance that gravity can pull the coaster down. Then, as the roller coaster goes down the hill, the potential energy is transformed into kinetic energy (the energy that takes you downwards.) After that, the roller coaster once again builds up its potential energy by going up another hill. As you can see, the roller coaster is actually continuously transforming potential energy to kinetic energy and vice versa.

My favorite roller coaster is the Behemoth at Canada's Wonderland, and it is a great example of a roller coaster transforming energy.

How to Add Vectors!

It seems that vectors is just one of those words that strikes fear in many students old and young alike. However, with the right fundamentals and techniques, the subject of vectors can be conquered without either extraordinary mathematics skills nor knowledge of physics. Before one can begin learning about vectors, he/she must first learn what a vector is. According to the Merriam Webster Dictionary, a vector is a variable quantity that can be resolved into component. To simplify this, here is an actual vector: 

A vector has three types of information: 1. the length
                                                            2. the angle
                                                            3. the direction


Now that we know what a vector is and what it signifies, we can start to conduct simple addition question for vectors.


If the vectors that we are adding have a distinct direction (North, South, East or West), then we just connect them. 

As you can see from this picture, the addition of vectors usually results in an imaginary triangle. After adding the horizontal component and the vertical component, you connect the origin to the ending point using a straight line. The first thing that you will need to calculate is the length of the hypotenuse. Due to the fact that you will know the lengths of the horizontal and vertical vectors, you can apply the Pythagorean Theorem:

Once you finish that, you will have the length of the vector. However, as I stated earlier, a vector has three components. Length is only one of the components. We also have to find the direction and the angle. To find the angle, we must measure angles with respect to North and South. If you are confused, simply draw a cross at the origin to display to you North, South, East and West. Now, you must apply simple trigonometry. Once you find out the right angle to measure, you can use tan, which is the length of the opposite side divided by the length of the adjacent side. Finally, you will have the angle. The last step is to simply state what direction the vector is going. To do this, you just need to look at the angle that you previously discovered. Since the angles are measured with respect to North and South, simply write East/West of North/South (whichever ones apply to your question)


Your end result should look somewhat like this: x=__m (N__ E)


And that's all you need to know about vectors for now!

Deriving Equation 4 from the Graph

Equation #4 is: d=V2Δt-½aΔt²

In order to derive the equation from the graph, we must find the area between the slope and the x axis. Unlike the steps for Equation 3, this time we must first find the area of the large rectangle and then subtract the smaller triangle from it.


The equation for the rectangle is ab, where a = base, and b= height. From the graph, we can determine the base and height of the rectangle. The length is Δt and the height is V2.

So, area of rectangle=V2(Δt)

To find the area of the triangle, we know that the equation is ab/2, where a is the base and b is the height. For the small triangle that we are going to use, it appears that its height is V2-V1, and its length is Δt.

So, area of triangle=½(V2-V1)Δt
                           
From Equation 1, we find that aΔt=V2-V1!

Substituting that into the equation gives us the following:

area of triangle=(½aΔt)Δt
                      = ½aΔt²

Finally, by subtracting the area of the triangle from the area of the rectangle, this gives us equation 4: 

d=V2Δt-½aΔt²

Deriving Equation 3 from the Graph

Equation 3 is: d=vΔt+½aΔt²

From the graph, we have V2, V1, t1, and t2.

In order to calculate the displacement, we have to find the area. We can do this in two ways: we can find the area of the triangle and the square, or we can find the area of the entire trapezoid. For this instance, I am going to find the area of the triangle and the rectangle.

The equation for calculating the area of a rectangle is a times b, where a is the height and b is the width.

From the graph, we can see that a=V1, and b=t2-t1.

So, A=(ab)
      A=V1(t2-t1)
      A=V1(Δt)

Now, we have to find the area of the triangle. The equation is a times b divided by 2, where a is the height and b is the length of the base. From this equation, we can find that it can also be expressed as 1/2ab.

From the graph, the base is Δt, and the height is V2-V1.

So, A=1/2Δt(V2-V1)

From Equation #1, we know that V2-V1= aΔt.

Therefore, A=1/2Δt(aΔt)
                 A=1/2aΔt²

So, because d(displacement)=area
Therefore finally, d=vΔt+½aΔt².

Translating Graphs from the Experiment

Here are the 6 graphs which have been translated. (Graph pictures courtesy of Daniel)

Graph 1 (Distance vs. Time)

1. Stay and don't move at a distance of 1m for 1 second.

2. Walk 1.5m in 2 seconds (0.75 m/s) away from the origin.

3. Stay at 2.5m for 3 seconds.

4. Walk 0.75m in 1.5 seconds (0.5 m/s) back towards the origin.

5. Stay at 1.75m for 2.5 s.

Graph 2 (Distance vs. Time)

1. Begin at a distance of 3m away from the origin. Walk back towards the origin at a rate of 1.5m in 3 s (0.5 m/s)

2. Stay at a distance of 1.5m for 1 s.

3. Jog back towards the origin at a rate of1m in 1 second (1 m/s).

4. Stay at a distance of 0.5m for 2 s.

5. Jog away from the origin at a rate of 2.5m in 3 seconds (0.83 m/s)



Graph 3 (Velocity vs. Time)

1. Don't move for 2 seconds.
2. Walk away from the origin at 0.5 m/s for 3 seconds
3. Stay still for 2 seconds.
4. Walk towards the origin at 0.5 m/s for 3 seconds.

Graph 4 (Velocity vs. Time)

1. Accelerate at 0.5 m/s in 4 seconds away from the origin.

2. Continue walking away from the origin at 0.5 m/s for 2 seconds.

3. Walk back towards the origin at 0.4 m/s for 3 seconds.

4. Stop and don't move for 1 second.

Graph 5 (Distance vs. Time)

1. Start at a distance of approximately 0.8m from the origin and walk away at a rate of 1m in 3.5 s (0.29 m/s)

2. Stay still at a distance of 1.8m for 3.25 s.

3. Continue walking away from the origin at a rate of 1.4m in 2.25 s (0.62 m/s)

Graph 6 (Velocity vs. Time)

1. Walk away from the origin at roughly 0.35 m/s for 3 seconds.

2. Walk back towards the origin at roughly 0.35 m/s for 3.5 seconds.

3. Don't move for 3.5 seconds.